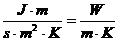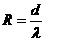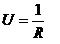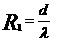Ehitusfüüsika õppematerjal

Materjalide soojajuhtivustegur

Soojusisolatsioonimaterjalide juures on üheks olulisemaks näitajaks soojusjuhtivustegur

λ (lambda). See on soojushulk, mis läbib 1m paksuse 1m2 suuruse materjali kihi 1 sekundi (s) jooksul, kui pindade temperatuuri vahe on 1°C  (1K).

Soojajuhtivustegur määratakse tootja poolt ja seda kinnitab viimase poolt deklareeritud sertifikaat.

Kui väljendada seda valemiga, siis näeb ta välja lõpptulemusena taandatud kujul järgmiselt:

Materjalikihi soojatakistus

Soojajuhtivusteguri kaudu on võimalik määrata kindlaks materjali ja välispiirde soojatakistus (R).

d - materjali paksus

λ - materjali soojajuhtivustegur

U väärtuse kaudu näidatakse soojavoolu ehk soojakadu läbi välisseina pinnaühiku kohta.

Seda mõistet kasutatakse projekteerimisel ja ehitamisel välispiirete soojakadude arvutamisel. Välispiirde normikohane U väärtus on 0,28 W/m²· K. Kuid viimasel ajal soovitatakse järjest soojapidavamaid seinu, mille U väärtus võiks näiteks olla juba vahemikus 0,12...20 W/m²·K.

Soojusjuhtivuse normatiive ja aruvtusmeetodeid võib leida standardist:

EVS EN 6946:2004 „Hoonete komponendid ja hoonekonstruktsioonid. Soojustakistus ja soojajuhtivus. Arvutusmeetodid”

Näide 1

Meil on elamu mille välisseinaks on Aeroc plokk EcoTerm Plus. Tehas annab selle materjali kohta oma sertifikaadis järgmised andmed.

Antud:

Ploki laius d = 375 mm = 0,375 mPoorbetooni soojaerijuhtivus λ = 0,088 W/m·k

Lisaks eeltoodust teame, et seina soojapidavuse arvutamisel võetakse aluseks seina sisepinna soojataksitus R_si ja välispinna soojatakistus R_{se .}

Alustuseks leiame seina soojatakistuse 

R_t = R_si + R₁ + R_se 

Kuna antud valemi lahendamiseks puudub meil R₁ ehk Aeroc'i soojatakistus, siis leiame kõigepealt selle.

                    R₁ = 0,375 : 0,088 = 4,26 m²·K /W   

Seina soojatakistus moodustub erinevate kihtide soojatakistuste summast.

                    R_t = 0,13 + 4,26 + 0,04 = 4,43 m²·K /W

Nüüd leiame seina soojajuhtivuse ehk U väärtuse.

                                         U = 1/R  

siit U = 1 : 4,43 = 0,23 W/m²·K

Nagu näeme rahuldab Aeroc plokist 375 mm paksune sein täielikult käesoleval hetkel kehtivad norme, kuna normatiivne U väärtus peaks olema 0,28 W/m²·K. 

Temperatuur välisseina erinevates kihtides

Kui me hakkame ehitama või restaureerima hoone välisseinu, siis on meil vaja teada temperatuuri seina erinevates kihtides. Seda sellepärast, et teaksime kus kohas võib tekkida seinas kastepunkt. Oluline on siin see, et kastepunkti tekkimist piirde sees tuleks vältida.  Kui see peaks tekkima võrdlemisi välispinna lähedal, siis tavaliselt  peale kütteperioodi lõppu - suvisel ajal, jõuab sinna mingil määral kogunenud niiskus siiski veel konstruktsioonist välja aurustuda. 

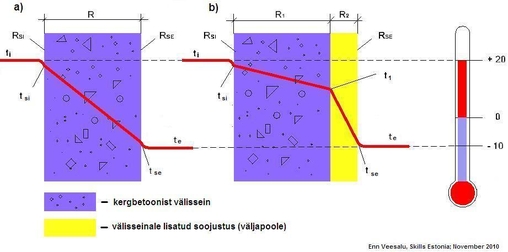
Joonis 2

 Kui me teame seina üldist soojatakistust (R_t)ja erinevate kihtide soojatakistusi siis on võimalik välja arvutada nii sise- (t_si), kui ka välispinnatemperatuur (t_se). Samuti seina kihtide vaheline temperatuur (t₁).

Tihti võib kohata olukordi, kus hoonete välisseina soojustusamisel võib kastepunkt, sattuda soojustuse taha ehk täpsemalt väljendades, jääb seina ja soojustuse vahele. Ning kui materjal ei lase niiskust läbi (näit. polüstürool), võivad hakata arenema seal suure niiskuskoormuse korral niiskuskahjustused.

Teeme näites 1 toodud andmetega ka selle kohta näidisülesande.

Näide 2

Nagu Joonise 2 a peal juba on kujutatud, valime toa sisemiseks  temperatuuriks t_i termomeetri näidu järgi +20°C ja välistemperatuuriks t_e -10°C.  Kuna meil on teada seina kogu soojatkistus R_t ja aerocploki soojatakistus R₁ ning seina sispinnatakistuse R_SI, välispinna soojatakistuse R_SE väärtused oleme varem võtnud juba tabelist. Seega on meil antud:

R_SI = 0,04 m²·K /W

R_SE = 0,13 m²·K /W

R₁ = 4,26 m²·K /W

R_t = 4,43 m²·K /W

t_i = +20°C

t_e = -10°C

Leiame:

t_si ja t_se  

Lahendus:

t_si = t_i - R_SI/R_t · (t_i - t_e) = 20 + 0,13/4,43 · (20-(-10)) = 20 - 0,88 = 19,12°C   

t_se = t_si - R₁/R_t · (t_i - t_e) = 19,12 - 4,26/4,43 · (20-(-10)) = 19,12 - 28,85 = -9,73°C

Kontroll:

Arvutuskäigu õigsust saame kontrollida nii, kui võrdleme seda, kas arvutuslik ja algandmetes antud t_e  langevad kokku.

t_e = t_se - R₁/R_t · (t_i - t_e) = 19,73 - 0,04/4,43 · (20-(-10)) = -9,73 - 0,27  = -10,00°C 

Vastus:

Nagu näeme  t_e = -10°C võrdsed nii algandmetes, kui ka kontrollimisel saadud arvutuliku tulemusena.

Joonise 2 b variandi puhul saame lahendada analoogiliselt ainult peame lisama välisseinale soojustuskihi, mille soojustakistuse tähistame R_{2 .} Selleks valime soojustuskihiks Paroc villast krohvialause soojustusplaadi paksusega d = 100 mm.

Tootja andmetel on sellise materjali soojusjuhtivustegur λ = 0,04 W/m·k.

Seega arvutame alljärgnevalt valemi (2) järgi soojustuskihi takistuse:

R₂ = 0,1 : 0,04 = 2,50 m²·K /W

Kuna nüüd muutub ka seina  üldine soojatakistus (soojapidavus), siis arvutame ümber ka valemi (3) järgi kogu välisseina soojatakistuse R_t

R_t = 0,13 + 4,26 + 2,50 + 0,04 = 6,93 m²·K /W

Ülejaanud andmed jäävad samaks, mis olid ka a variandi puhul.

R_SI = 0,04 m²·K /W

R_SE = 0,13 m²·K /W

R₁ = 4,26 m²·K /W

R₂ = 2,50 m²·K /W

R_t = 6,93 m²·K /W

t_i = +20°C

t_e = -10°C

Leiame:

t_si ; t₁ ja t_se  

Lahendus:

t_si = t_i - R_SI/R_t · (t_i - t_e) = 20 + 0,13/6,93 · (20-(-10)) = 20 - 0,56 = 19,44°C   

t₁ = t_si - R₁/R_t · (t_i - t_e) = 19,44 - 4,26/6,93 · (20-(-10)) = 19,44 - 18,44 = 1,00°C

t_se = t₁ - R_se/R_t · (t_i - t_e) = 1,00 - 2,50/6,93 · (20-(-10)) = 1,00 - 10,82 = -9,82°C

Kontroll:

Arvutuskäigu õigsust saame kontrollida nii, kui võrdleme seda, kas arvutuslik ja algandmetes antud t_e  langevad kokku.

t_e = t_se - R₁/R_t · (t_i - t_e) = -9,82 - 0,04/6,93 · (20-(-10)) = -9,82 - 0,17  = -9,99°C ≈

≈ -10,00°C 

Märkus:  0,01°C viga tekkis arvutuste ümmardamisel. Kui need samad arvud panna Exceli tabelise, siis tuleb välja täpselt, ilma parandusteta.

Vastus:

Nagu näeme on ka selles lahenduses  t_e = -10°C võrdsed nii algandmetes, kui ka kontrollimisel saadud arvutuliku tulemusena

.